This is a webified version of my paper from the
Proceedings of Bridges 2007
Modular Kirigami
George W. Hart
Computer Science Department
Stony Brook University
Stony Brook, NY 11794 USA
http://www.georgehart.com
Abstract
Modular Kirigami is here defined as the symmetric assemblage, with artistic intent, of multiple copies of cut paper shapes. Intricate examples with icosahedral symmetry are presented. These consist purely of interlocked flat pieces of paper, with no folding and no adhesives.
Introduction
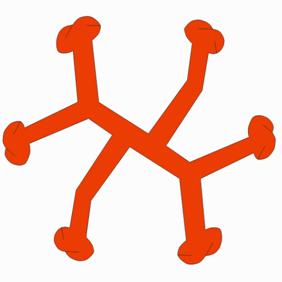
Kirigami refers to the art of paper cutting. Traditionally a single sheet of paper is cut with scissors or a knife to make a figurative or abstract form. [8, 10] The visual focus may be either the cut paper or the remaining “negative space”. Sometimes folding is involved, as in “pop-up cards”. [1] For symmetric designs, the paper is often folded before cutting then unfolded, e.g., the well-known paper snowflakes with 6-fold symmetry. Kirigami shares the root gami, meaning paper, with the better-known Japanese art of folding paper, origami. [7] In modular origami, identical paper modules are folded and assembled into a larger symmetric structure. [3] This paper introduces the term modular kirigami for symmetric assemblages of cut paper. Figure 1 shows an example constructed of twelve identical paper parts.
|
|
|
|
Figure 1a. Deep Sea Tango, 12 parts, 4 in |
Figure 1b.
Part design |
As of this writing, (December 2006) Google reports fourteen million hits for the word “origami”, one hundred thousand hits for “kirigami”, thirty-two thousand hits for the phrase “modular origami”, and zero web pages with the phrase “modular kirigami”. So I’ll claim credit for this neologism, but examples of assembling cut pieces of paper into symmetric structures are common. For example, any schoolchild who has cut out twelve regular pentagons and glued or taped them together into a model of a dodecahedron has assembled cut pieces of paper into a symmetric form. However, what is presented here as modular kirigami differs in having both an artistic intent for the design and a purity of technique.
Origami purists eschew cutting, taping, and gluing—only folding is allowed. Analogously, this essay focuses on a pure form of modular kirigami in which no folding, taping, or gluing is used—only cutting. Furthermore, the paper in all the examples shown is purely flat, not curved, e.g., not bent into a cylinder. However, the paper may need to be bent and then unbent during assembly, to achieve an intricate weave, as illustrated in Figure 2.
|
|
|
|
Figure 2a. Tangled Reindeer, 12 parts, 5 inch |
Figure 2b. Part design |
This form of modular kirigami is related to many sculptures I have made, which are assembled from planar rigid components. [6] I often make paper models of designs before making the actual sculpture from materials such as wood, metal, or acrylic. I may glue or tape paper models of my sculpture, because their function is only to help me visualize and further develop the final form. But the kirigami presented here are the final form: sculptures designed for paper. They specifically recognize two material properties of paper: (1) The flexibility of paper is essential to the design because during assembly, the components are interwoven. But once positioned they spring back into the paper’s natural planar form. (2) The surface friction of paper holds parts together. This is important in slot-based connections. If made of a slippery material, some of these designs could spontaneously disassemble and fall apart when handled.
These designs are also related to cut-and-assemble geometric constructions that I have called “Slide-Togethers” [4]. But the slide-togethers have regular polygon shapes for the components, e.g., pentagons or pentagrams with slots. In contrast, the modular kirigami presented here have parts designed for an aesthetic impact. Of course, they also must satisfy many geometric constraints in order to fit together symmetrically. Another related type of geometric kirigami is what John Sharp calls a sliceform, a slot-based construction, not necessarily symmetric, of non-identical parts [9].
One of the geometric details to work out for each design is the slot width for parts to fit together snugly. Slots need to be cut according to the thickness of the paper that fills the slot. If the slots are too thin, the paper may deform. If too wide, the joints will freely disassemble. This parameter does not scale with the 2D part dimensions. For example, software design tools let you easily scale a part file to be twice as big, but this will change a snug-fitting part into a loose part, unless one either does not scale the slot or compensates in the third dimension by using paper twice as thick. This is an issue common to all slot-based paper constructions.
Although I am a purist about the designs shown—there is no folding, no tape, and no glue—I am not a purist about the execution of the cutting. Rather than laboring intensely with knife or scissors to cut the parts manually, I am very happy to use modern computer-controlled cutting technology to produce the individual parts. Having made a great many paper models throughout my life, I know that cutting is lengthy work if done by hand. Automated paper cutters can do this repetitive work and thereby make the overall job much more enjoyable. I design, a machine cuts the paper, and I have the tricky task of assembling the parts, which I find to be an enjoyably challenging recreation. For example, I would not want to hand cut the twenty deeply curved parts of Figure 3, but it was very satisfying to assemble.
|
|
|
|
Figure 3a. Meanders, 20 parts, 5 inch |
Figure 3b. Part design |
Two types of automated processes are available for cutting paper parts. The first is to prepare a cutting die that is used to stamp out the parts. This involves a large initial investment, but then fast production with a low per-part cost. While ideal for mass production, stamping dies are not appropriate for experimental designs or low-volume production, because of the high initial tooling cost. The second method involves a “cutting plotter” which traces out each part with a computer-controlled knife. Various commercial and professional machines are available for this purpose, typically used in signage, e.g., to fabricate vinyl stick-on letters. Recently, less expensive home-use machines have become available. I have purchased a Graphtec “Craft ROBO” [2] and used it to cut all the parts for the examples shown in this paper.
I should point out that the machine is not as simple to use as, say, a printer or paper shredder. One does not just feed in a sheet of paper at one end and collect cut parts emerging out the other end. I went through considerable experimentation with various types and weights of paper. Knife depth and speed settings must be adjusted for the stock. A sticky carrier sheet, with a surface like “Post-It” glue, holds the paper and parts as they are cut. The parts and scrap paper must be carefully lifted and peeled off this carrier when done. The weight, consistency, and sizing of the stock greatly affect the result. There are some technical issues concerning sharp corners and small details. But after mastering the capabilities of the machine, I have found it to be quite accurate, great fun, and artistically empowering.
Before acquiring the automatic cutter, I had cut parts for similar designs in one of two ways: either individually with scissors, which is very time consuming, or by the ream on a band saw. The band saw method is useful if making intricate parts for an entire class to use in a paper construction workshop, so I’ll describe it here. Place a ream of (8.5 by 11 inch) card stock on a piece of (8.5 by 11 inch) quarter-inch plywood. On top of the paper, put a copy of the template to cut. Then drill holes through the stack and screw everything together with flat-head screws facing upwards. The heads are countersunk up into the bottom of the plywood. The screw threads protrude at the top, and a washer and nut secure the template and paper to the wood. Cut through this entire stack on a band saw, following the lines of the template on top. The screws, which are positioned in the scrap part of the paper, are carefully cut off as the last step, so everything remains registered together throughout the process.
Issues of artistic reproducibility arise when a cutting machine is involved. From the templates given as figures here, or from my original computer files, anyone might use a similar machine to replicate the paper components. Given the same paper, those parts might then be assembled into a sculpture indistinguishable from my original. How do I feel about that? The perceived value of fine art lies partly in its uniqueness or limited availability. But machine-cut parts, like digital media, are easily reproduced. So are these modular kirigami art? My feeling is that they are art, but perhaps not valuable art. The art is more in the design than the execution. I am prouder of the intellectual property of the designs than of the particular paper embodiments illustrated. However, I’ll note that considerable skill in assembly is needed—they are much harder to build than they look. In fact, I wonder if anyone but me could assemble all of these designs. If someone does replicate any of these designs, I would wish the copy to be labeled “Copy by X of a design by George W. Hart”. This would distinguish their assemblage from my original, which might be especially useful in the future, if it turns out that they assembled the parts incorrectly.
|
|
|
|
Figure 4a. Bones, 30 parts, 5 inch |
Figure 4b. Part design |
Mathematically, any type of spatial symmetry might be used as the foundation for modular kirigami. The examples in this paper all have icosahedral symmetry without mirrors. The order of this symmetry group is sixty, so by Lagrange’s theorem, the number of identical parts in any of these designs must be a divisor of sixty. If there are n identical parts and each has k-fold symmetry, then n∙k=60. For example, in Figures 1 and 2 there are twelve 5-fold parts and in Figure 3 there are twenty 3-fold parts. Another possibility is found in Figures 4 and 5, which each have thirty 2-fold parts. Examples below illustrate the remaining possibility: sixty parts with no rotational symmetry. There are no other possibilities, because the rotational order of a part must divide into the order of one of the symmetry axes. For example, there can not be fifteen 4-fold parts because the icosahedral group only has 2-fold, 3-fold, and 5-fold axes. (Of course, 4-fold parts are possible in a form with other symmetries, e.g., octahedral, not illustrated in this paper.) The symmetry also constrains the possible symmetric color patterns, as discussed in connection with particular examples in the following section.
|
|
|
|
Figure 5a. Monsters, 30 parts, 5 inch |
Figure 5b. Part design |
Description of Examples
Part a of each figure is the paper kirigami sculpture. Each example is made of commercially manufactured acid-free colored card stock in various weights up to 220 gr/m2. Part b of each example is the template for one part. When holding the model and turning it in one’s hands, the viewer experiences a visual Gestalt shift between seeing the repeated parts and seeing the whole.
Figure 1 shows Deep Sea Tango, an adaptation to paper of a sculpture that I first made in acrylic plastic. [5] In the acrylic version, the twelve identical parts are glued together at their tips. In the paper version, slots near the tips of the arms hold everything together and friction keeps the parts from disconnecting. The rigid acrylic version is barely possible to assemble, because the arms are always in each other’s way. For the paper version, I made the arms slightly longer to allow for the slots. With this extra length, it would not be possible to assemble with rigid parts. However, the paper arms are easily bent to bypass each other, so it is merely tricky, not impossible, to assemble. For this instance of the design, I used paper of a single color. But as it is based on the faces of a dodecahedron, it could also be made nicely with six colors, using one color for each pair of opposite parallel components. I have cut parts for ten copies of this design, and given kits with an instruction sheet to various friends, for them to assemble. But after several months, no one has reported success. This suggests that these designs may be too complex to consider commercializing as do-it-yourself assembly kits, although the difficulty may lie in my instructions.
Tangled Reindeer, shown in Figure 2, is a paper adaptation of a sculpture that I first made with solid freeform fabrication technology. [5] The paper version in Figure 2 is made from a metalized card stock, which is white on the inside with a gold foil surface on the outside. Because of the deep intermeshing of the components, it would be totally impossible to assemble with rigid parts. However, the flexibility of paper makes it possible. Even though I designed it, I find it confusing, as evidenced by the fact that it took me two hours to assemble, using tweezers to manipulate the small connecting tips.
Figure 3 illustrates Meanders. This design has twenty parts, each of which connects to six others, while forming a knitting-like weave. Above the center of each part is connection of three neighboring parts. This type of three-way interlocking joint is very stable and will not fall apart. Each of the three mating parts keeps the other two from unlocking. Conversely, it takes some nimble finger work to get each set of three together. And of course, the paper parts must be bent considerably during assembly to weave them through each other properly. A small triangular hole in the center of each part is hidden behind each joint, not visible until one looks closely.
|
|
|
|
Figure 6a. Windmills, 32 parts, 4 inch |
Figure 6b. Part design |
The same type of three-way interlocking joint is used in Figure 4, Bones. This design is rather more intricate, with sixty joints instead of twenty. Probably it would be more understandable with multiple colors. Each component has twelve connecting slots, but connects to only eight different components, because it doubly connects to some. In assembling a sculpture like this, I typically go through a series of psychological stages. It is very easy to connect the first two or three parts, because I know exactly how the local connections are designed. When I continue adding parts, it soon becomes difficult, because in a state of partial completion, much of the context is missing so it becomes unclear what should go in front or behind of what. But after I’m quarter or half finished, I get a good hands-on understanding of the structure and it becomes easy again. Then when it is nearly complete, there are new physical difficulties of getting inside to reach where I need to, with the interior closed off. And finally, when the last piece is positioned, it all seems so easy, as I really understand the structure intellectually and tactilely, and can see each part in the context of its neighbors.
Monsters, in Figure 5, consists of thirty identical dinosaur-like parts. There are six parts in each of five colors. The coloring is based on the compound of five cubes inscribed in a dodecahedron. The six parts of any given color lie, parallel and perpendicular, in the planes of an imagined cube. Each part joins with four others, in the other four colors. Unfortunately, the long necks result in a somewhat flexible structure. I feel the form would be better instantiated in a more rigid material, such as metal.
Figure 6 shows Windmills. This design has two types of part that interlock very densely: twelve red five-fold windmills and twenty yellow three-fold windmills. The five-fold parts lie on five-fold axes of symmetry and the three-fold parts lie on three-fold axes of symmetry. But it is so dense that one can nowhere see a complete part, and one can not view through the interior to see the back of parts on the other side. In person, I find it creates in the viewer a peculiar optical effect in which the eye assumes there is only one type of part, which is red on one side and yellow on the other side. This is a novel optical illusion that I have not seen described elsewhere.
|
|
|
|
Figure 7a. Arrows, 60 parts, 7 inch |
Figure 7b. Part design |
Figure 7 shows Arrows. Here there are sixty parts with no symmetry to each part. It is made with ten parts in each of six colors. The ten arrows of each color form two circles of five, in two parallel planes. Parallel circles rotate in opposite directions around a common axis. This form is a development of a six-foot diameter wooden sculpture I made for Burning Man 2006, but that did not use arrows or colors. That sculpture was inspired by some designs by the sculptor Rinus Roelofs, who was in turn inspired by some designs in the notebooks of Leonardo da Vinci.
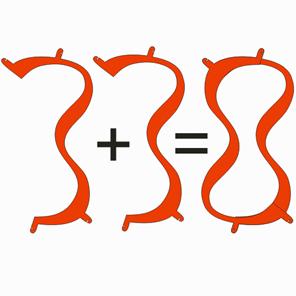
Finally, Figure 8 shows Eights, made of thirty “8”-shaped loops. The loops are linked, so could not be assembled from uncut loops. I made each “8” from two “3”-shaped parts that overlap to form an “8”. Curiously, 3+3=8. Using slotted tabs, each “8” mates with four other “8”’s of the same color. So there are actually sixty parts, each with no symmetry, which overlap in pairs to make thirty apparent parts with 2-fold symmetry. This was extremely difficult to assemble, taking me four hours to complete after several false starts. With some bravura, I’ll wager a beer that no one else in the world would have the obsessive-compulsive patience to assemble it at all!
|
|
|
|
Figure 8a. Eights, 60 parts, 5 inch |
Figure 8b. Part design |
Conclusions
Modular kirigami was introduced, consisting of symmetric arrangements of cut paper, assembled purely, with no glue. Intricate sculptural examples with icosahedral symmetry were presented. The field is wide open for others to develop further, as many other styles, symmetries, and joint designs are possible. I expect to see an explosion of ideas in the future, as inexpensive cutting plotters remove the tedium from the medium.
References
[1] Laura Badalucco, Kirigami: The Art of 3-dimensional Paper Cutting, Sterling, 2001.
[2] Graphtec, Craft ROBO, http://www.graphteccorp.com/craftrobo and http://www.craftrobostore.com
[3] Rona Gurkewitz and Bennett Arnstein, Multimodular Origami Polyhedra: Archimedeans, Buckyballs and Duality, Dover, 2003.
[4] G. Hart, “‘Slide-Together’ Geometric Paper Constructions”, Teachers' workshop at Bridges Conference, 2004, available online at http://www.georgehart.com.
[5] G. Hart, “Sculpture from Symmetrically Arranged Planar Components”, Proceedings of Bridges 2003, Granada Spain, pp. 315–322.
[6] G. Hart, “Symmetric Sculpture”, to appear in Journal of Mathematics and the Arts, 2007.
[7] Robert Lang, Origami Design Secrets: Mathematical Methods for an Ancient Art, A.K. Peters, 2003.
[8] Jeffrey Rutzky, Kirigami, Barnes and Noble, Inc., to appear, Fall 2007.
[9] John Sharp, Sliceforms: Mathematical Models from Paper Sections, Tarquin, 1997.
[10] Florence Temko, Origami and Kirigami, Dover, 2006.
Note
The designs illustrated are for academic use only. Commercial use without the written permission of the author is prohibited. Thank you Jeffrey Rutzky for showing me the Craft ROBO and for comments on a draft of this paper.