This paper appeared in the
June 2002 issue of
Humanistic
Mathematics Network Journal, pp. 3-5
Loopy
George W. Hart
http://www.georgehart.com
As a mathematician and sculptor, I try to create artworks that are infused
with an underlying sense of pattern and structure. See [1]-[9]. I hope
that viewers of my sculpture will consciously or unconsciously develop
an appreciation for the power of mathematical ideas to enrich art. Ideally,
they will be inspired to try their own explorations in the area of mathematical
art. This paper considers one sculpture in some detail and provides instructions
for a paper model that lets one explore its structure.
 Figure
1 shows a sculpture I call Loopy, made of painted aluminum. It is
five feet in diameter, and stands eight feet tall on its steel base. I
created it for an outdoor setting at a local hospital; it is intentionally
colorful and joyous. There are thirty identically shaped loops, six in
each of five bright colors: red, orange, yellow, green, and blue. My vision
of the form is abstract; some viewers tell me they see it as a giant brain,
but that was not a conscious intention of mine. ("No, it isn't a self-portrait,"
I tell people.)
Figure
1 shows a sculpture I call Loopy, made of painted aluminum. It is
five feet in diameter, and stands eight feet tall on its steel base. I
created it for an outdoor setting at a local hospital; it is intentionally
colorful and joyous. There are thirty identically shaped loops, six in
each of five bright colors: red, orange, yellow, green, and blue. My vision
of the form is abstract; some viewers tell me they see it as a giant brain,
but that was not a conscious intention of mine. ("No, it isn't a self-portrait,"
I tell people.)
On examination, most viewers can discover and articulate essential aspects
of the structure and color pattern: Each loop crosses four loops of the
four other colors. The ends of the loops always meet in groups of three
of the same color. Around each five-sided opening, there is a spiral of
five loops, one in each of the five colors. No loop crosses another of
the same color. Each bolt is the both the vertex of a regular pentagon
and the midpoint of the side of an equilateral triangle.
Each loop began as a ten-foot long strip of aluminum that was drilled
for bolt holes, rolled into a loop, primed, painted, and bolted into the
assembly. Thus, the thirty strips together sum to 300 feet, the length
of a football field. While this arithmetic may be impressive in its own
way, there is a different sort of mathematical analysis that I wish to
emphasize.
Another sort of calculation one could make concerning the sculpture
is to determine the angle at which the loops cross. Knowing only that the
bolt holes are equally spaced and each loop is part of a great circle,
it is possible with a bit of spherical trigonometry to calculate the angle
at which loops meet. Pleasantly, it is not necessary to solve this, as
the components automatically position themselves at the proper angle. This
is analogous to cutting out twenty equilateral triangles and taping them
together into an icosahedron. One does not need to know the dihedral angle
of an icosahedron beforehand; the model automatically rigidifies to the
necessary dihedral angles as the last edges are joined.
The mathematical properties that I consider most worthy of attention
involve the structure and coloring. I do not know that I can articulate
the intuitive reasons why I feel they are worth study. Perhaps the sculpture
itself addresses that ineffable issue. But I do predict that if the reader
or a student makes the following paper model, they will come to share some
of this understanding. Loopy has a two-layer structure, which for
architectural simplicity, this paper model simplifies to just one layer.
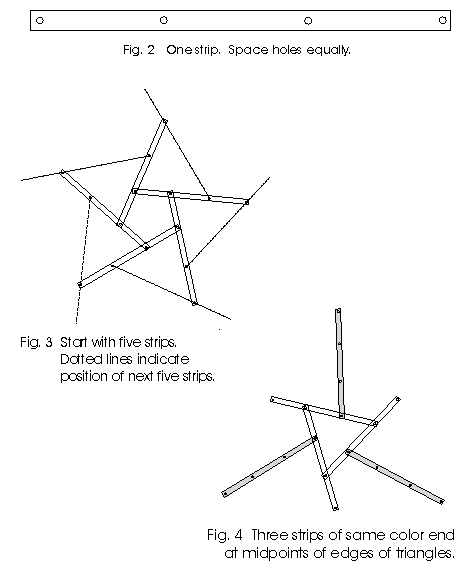 Cut
out thirty strips of heavy paper, e.g., poster stock. Eleven inches by
one-half inch is a convenient size if one starts with U.S. standard 8.5x11
inch paper. A paper cutter makes quick work of this. There should be six
strips in each of five different colors. Use a hole puncher to make four
equally spaced holes in each, as shown in Figure 2. Paper fasteners will
be used to join the strips. They allow free rotation, and the proper angle
will form on its own.
Cut
out thirty strips of heavy paper, e.g., poster stock. Eleven inches by
one-half inch is a convenient size if one starts with U.S. standard 8.5x11
inch paper. A paper cutter makes quick work of this. There should be six
strips in each of five different colors. Use a hole puncher to make four
equally spaced holes in each, as shown in Figure 2. Paper fasteners will
be used to join the strips. They allow free rotation, and the proper angle
will form on its own.
Begin by making a fivefold spiral as in Figure 3, using five different
colors. The placement of the next five strips is indicated by the dotted
lines. Note that the pentagon edges are one unit long but the triangle
edges are two units long. Each strip has two "end holes" and two "inner
holes." Each paper fastener connects one end hole and one inner hole. For
a maximally attractive model, consistently place the end hole inside (underneath)
the inner hole it joins. The assembly and coloring of the remainder of
the model is then determined by logically keeping in mind three rules:
-
Every opening is either a pentagon with edge length one or a triangle with
edge length two;
-
Each pentagon is surrounded by five triangles;
-
The three strips that touch any triangle's edge midpoints are of a single
color. See Figure 4.
In building this model, one will appreciate that there is a fundamental
structure inherent in it. Why does it work? For example, why is one never
forced into a situation where a strip touches another of the same color?
Or why doesn't one come to a point around back where a triangle's midpoints
contact endpoints of more than one color? A full explanation would involve
a discussion of how the group of tetrahedral rotations is a subgroup of
the icosahedral group. If the geometric model known as "the compound of
five tetrahedra" were better known, a study of its thirty edges could serve
as a basis for understanding Loopy; each presents five groups of
six. Similarly, one might wonder at how the paper strips work together
as an analog computer, to solve the equation of the angle crossing. As
I came to the form intuitively before doing any mathematical analysis,
my feeling is that thinking about these questions goes hand in hand with
just seeing that the form is beautiful.
For a well-rounded education, it is important that students develop
the ability to discover new truths on their own. Let me suggest a few ideas
for those who wish to start with this model and then explore further: Loopy
has small pentagons and large triangles; try making the pentagons twice
the edge length of the triangles. Notice you can start with a left-handed
or right-handed spiral of five strips; what happens if you turn your model
inside out? Or, try making a four-color structure with squares instead
of pentagons. Or, design an analogous structure in which all the openings
are triangles. Or, explore other color patterns. Can you generalize any
of these models to a structure with hundreds of components? These questions
might engage curious students.
For me, one key aspect of the math-art connection is that both can concern
space, and patterns or structures in space. Both also involve aesthetics
in a hard to define manner, which involves much subjectivity. But a theorem
or proof of Euclid's can be simply beautiful, and a mathematician sees
this as clearly as an artist sees that a line by Leonardo can be simply
beautiful. Both fields also involve creative individuals who find satisfaction
in creating and communicating new forms that are the outward expression
of their inner visions. I feel Loopy and my other constructive geometric
sculptures are somewhere in this common tradition, and I hope viewers can
appreciate the synthesis. Mathematics is about patterns, structures, and
relationships of all kinds. Art as much as anything can bring this out.
References
[1] G.W. Hart, Geometric Sculpture, http://www.georgehart.com/
[2] G.W. Hart, "Icosahedral Constructions," in Proceedings of Bridges:
Mathematical Connections in Art, Music and Science, Southwestern College,
Winfield, Kansas, July 28-30, 1998, pp. 195-202.
[3] G.W. Hart, "Zonish Polyhedra," Proceedings of Mathematics and
Design '98, San Sebastian, Spain, June 1-4, 1998.
[4] G.W. Hart, "Reticulated Geodesic Constructions," Computers and
Graphics, 24(6), Dec. 2000, pp. 907-910.
[5] G.W. Hart, "The Millennium Bookball," in Proceedings of Bridges
2000: Mathematical Connections in Art, Music and Science, Southwestern
College, Winfield, Kansas, July 28-30, 2000.
[6] G.W. Hart, "Sculpture Based on Propellorized Polyhedra," Proceedings
of ISAMA 2000, International Society of Art, Math, and Architecture,
Seattle, August, 2000.
[7] G.W. Hart, "Computational Geometry for Sculpture," Proceedings of
ACM Symposium on Computational Geometry, Tufts University, June 2001.
[8] G.W. Hart and Henri Picciotto, Zome Geometry: Hands-on Learning
with Zome Models, Key Curriculum Press, 2001.
[9] G.W. Hart, "The Geometric Aesthetic," in The Visual Mind 2,
Michele Emmer (ed.), MIT press, to appear.
 Figure
1 shows a sculpture I call Loopy, made of painted aluminum. It is
five feet in diameter, and stands eight feet tall on its steel base. I
created it for an outdoor setting at a local hospital; it is intentionally
colorful and joyous. There are thirty identically shaped loops, six in
each of five bright colors: red, orange, yellow, green, and blue. My vision
of the form is abstract; some viewers tell me they see it as a giant brain,
but that was not a conscious intention of mine. ("No, it isn't a self-portrait,"
I tell people.)
Figure
1 shows a sculpture I call Loopy, made of painted aluminum. It is
five feet in diameter, and stands eight feet tall on its steel base. I
created it for an outdoor setting at a local hospital; it is intentionally
colorful and joyous. There are thirty identically shaped loops, six in
each of five bright colors: red, orange, yellow, green, and blue. My vision
of the form is abstract; some viewers tell me they see it as a giant brain,
but that was not a conscious intention of mine. ("No, it isn't a self-portrait,"
I tell people.)
 Cut
out thirty strips of heavy paper, e.g., poster stock. Eleven inches by
one-half inch is a convenient size if one starts with U.S. standard 8.5x11
inch paper. A paper cutter makes quick work of this. There should be six
strips in each of five different colors. Use a hole puncher to make four
equally spaced holes in each, as shown in Figure 2. Paper fasteners will
be used to join the strips. They allow free rotation, and the proper angle
will form on its own.
Cut
out thirty strips of heavy paper, e.g., poster stock. Eleven inches by
one-half inch is a convenient size if one starts with U.S. standard 8.5x11
inch paper. A paper cutter makes quick work of this. There should be six
strips in each of five different colors. Use a hole puncher to make four
equally spaced holes in each, as shown in Figure 2. Paper fasteners will
be used to join the strips. They allow free rotation, and the proper angle
will form on its own.