|
|
|
|
Abstract
A "propellor" operation for constructing interesting new polyhedra is defined and demonstrated. Examples include the five "propello-Platonics," based on the Platonic solids but with each face surrounded by a "propellor" of tetragons. Each has the rotational symmetry of its underlying Platonic solid, but comes in left- and right-handed forms. The simplest example, the propello-tetrahedron, has 16 faces (4 triangles, 12 tetragons) and is self-dual. The operation can be applied to any convex polyhedron, and combined with other operations to produce a wide variety of new forms. These provide a storehouse of intriguing structures, some of which have inspired artworks. Templates for a paper model are provided. Sculptures by the author based on some of these new forms are illustrated, involving a variety of media, including wood, CDROMs, and stereo-lithography.
Introduction
As a sculptor of constructive geometric forms, I try to create engaging works that are enriched by an underlying geometrical depth. A carefully chosen mathematical form not only provides structure, balance, and symmetry, but also provides the framework for an internal coherence that viewers may appreciate unconsciously even if they do not consciously recognize all the patterns or relationships present. I work with a variety of media, and in each piece I choose materials to complement the underlying geometrical form. [1-9] The sculpture Rainbow Bits, Figure 1, is composed of 642 CDROMs, arranged along the edges of a "midscribed propellorized icosahedron," described in detail below. Figure 2 is a wooden construction based on the same underlying polyhedron.
|
|
|
|
 |
|
|
While viewers sometimes describe my pieces as spheres, I see them not as spheres, but on spheres. One does not say that oil painters paint rectangles, but they do paint on rectangles. Similarly, I see the sphere as a canvas to sculpt upon. From the designer's perspective, the sphere presents a challenging constraint, because there is no convenient edge to the canvas. The sculpture must close upon itself in a coherent manner. For this purpose, knowledge of polyhedral forms can provide a useful framework.
This paper describes a polyhedron operator that I call the "propellor" operator, which creates a new polyhedron from any given convex polyhedron. It is intentionally spelled so as to distinguish it from "propeller". Introductory examples demonstrate its operation on the Platonic solids. Several geometric variations of the results are presented. A system of other polyhedral operators is sketched and some relations involving the operation are presented. Finally, sculptures based on these results are illustrated. Proofs of the mathematical results are left for the appendix.
The Propellor Operator
The propellor operator is fundamentally a topological operation—it determines
an arrangement of vertices, edges, and faces that it produces. It does
not determine the geometric realization of its output—the exact lengths
and angles. This section describes the topology and the following section
illustrates three choices of geometric realization.
 |
|
|
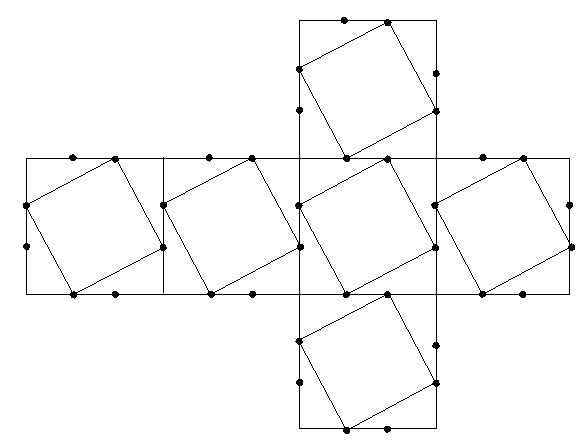
As an example, consider the cube. Figure 3 shows the net of a cube,
unfolded into six squares. Each edge of the cube is marked with dots indicating
new vertices that divide it into three segments. To carry out the propellor
operation on the cube, one uses these new vertices and adds four lines
inside each square face, to create a smaller square within each square.
As figure 4 suggests, the smaller squares must all be made with the same
direction of rotation —all clockwise or all counterclockwise—so there are
two possible mirror image forms. For the second form, look at Figure 4
in a mirror.
 |
|
|
The net of a propello-cube, illustrated in figure 4, consists of six (small) squares and 24 tetragons. The tetragons are the four areas around each small square. They appear as right triangles in Figure 4, but topologically they are quadrilaterals, bounded by four vertices and four edges. In the geometric realizations presented below, the tetragons will be more obviously four-sided.
 |
 |
|
|
|
For the general process, we start with any polyhedron, place two new vertices on each edge, then create in each n-gon face a smaller n-gon, always choosing a consistent handedness. For example, if we started with any polyhedron consisting of triangles (e.g., a tetrahedron, octahedron, or icosahedron) we would propellorize it by replacing each of its faces with a smaller rotated triangle surrounded by three tetragons, in the pattern of Figure 5. Figure 6 shows the net of the result of propellorizing the regular tetrahedron.
So far, these constructions are not geometrically interesting. For example, if the propello-cube net of Figure 4 were to be folded back up into a cube, it would look just like a cube with extra lines drawn on its faces. To make interesting new polyhedra, we next adjust the lengths and angles of these forms, while maintaining this topological connectivity.
Three Geometric Realizations of the Propello-Platonics
There are infinitely many geometrically distinct forms with the same topological structure. (Imagine stretching a rubber polyhedron model.) Each propello-Platonic realization in this section has the rotational symmetries of its underlying Platonic solid, without the mirror symmetries. We use the notation pT to refer to any propello-tetrahedron, i.e., any polyhedron with the same topological structure as the object unfolded to make Figure 6. We begin by illustrating three special geometric forms of the pT: one inscribed, one midscribed, and one circumscribed to a sphere.
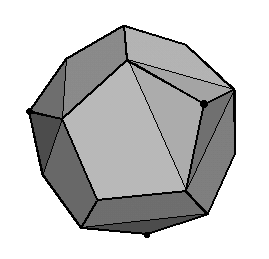
Inscribed. Figure 7 illustrates a pT construction
starting with a regular dodecahedron. It is well known that one can choose
four vertices of the dodecahedron which are positioned as the vertices
of a regular tetrahedron. Three are marked in Fig.7 and one is around the
back. The thinner lines show where to truncate four such vertices of the
dodecahedron, cutting off triangular pyramids so deep as to contact the
adjacent vertices of the dodecahedron. This creates four new triangular
faces and changes the twelve pentagons into tetragons. This structure of
four triangles and twelve tetragons is a pT. Because the dodecahedron's
vertices lie on a sphere, the resulting pT of Figure 8 can be inscribed
in a sphere. The tetragons have the special property of being tri-equilateral
trapezoids, meaning three of the edges in each tetragon are equal, because
they are all edges of the original dodecahedron. A nice model can be constructed
with ZomeTools [9]. The shape can be generalized by distortions that change
the ratios of the sides, yet maintain the polyhedral symmetry and keep
the tetragons flat.
 |
 |
|
|
|
Circumscribed. Figure 9 illustrates a pT construction
starting with a regular icosahedron. It is well known that one can choose
four faces of the icosahedron which are in the planes of a regular tetrahedron.
Two of these can be seen, darkened, in Fig. 9. The thinner lines show where
to erect a pyramid upon four such faces of the icosahedron, choosing their
height so that the pyramid faces extend the adjacent faces of the icosahedron.
The effect is to eliminate four of the icosahedron's twenty faces and convert
twelve others into tetragons. Four of the icosahedron's triangles remain
unchanged. Because the sixteen faces are all in planes of the underlying
icosahedron's faces, the resulting pT of Figure 10 can be circumscribed
about a sphere. The tetragons have the special property of being kites,
meaning one of their diagonals is a mirror line. This polyhedron is Zometool
constructible with blue and green struts. It also can be generalized by
distortions that change the ratios of the sides, yet maintain the polyhedral
symmetry and keep the tetragons flat.
|
|
 |
|
|
|
Midscribed. Figure 11 illustrates the midscribed version of the pT, meaning every edge is tangent to a unit sphere. I know of no simple geometric construction that produces it. However, it can be constructed numerically by an iterative procedure described in [5] or exactly by solving a set of simultaneous polynomial equations. The special form of the tetragons in the pT of Figure 11 is that they are tri-equiangular kites, meaning that three of each kite's angles are equal. Unlike the previous two cases, there is no distortion which can change the edge lengths while maintaining the underlying symmetry and keeping the tetragons planar.
 |
|
|
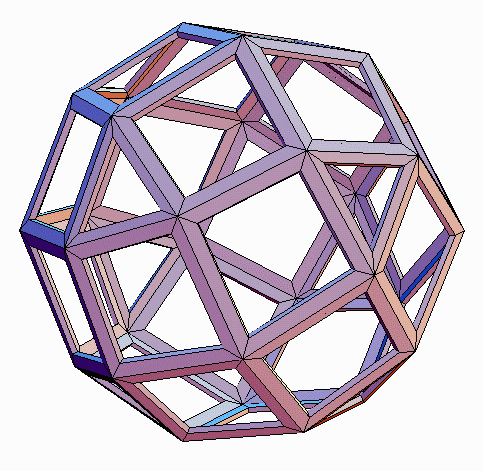
For comparison, Figures 8, 10, and 11 show these three forms of the
pT,
rendered in Leonardo da Vinci's open-face style of presentation. This allows
one to see the face planes and also to see through the faces to the rear
surface. One can verify that all three pT forms are topologically
identical to that of Fig. 6. Each consists of four propeller-like groups
of an equilateral triangle surrounded by three tetragons. The pT
is topologically self-dual. The circumscribed and inscribed versions are
geometrically dual to each other (reciprocals in a sphere) and the midscribed
version is geometrically self-dual.
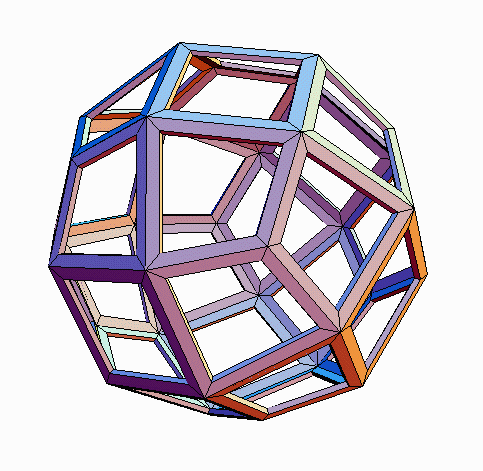 |
 |
|
|
|
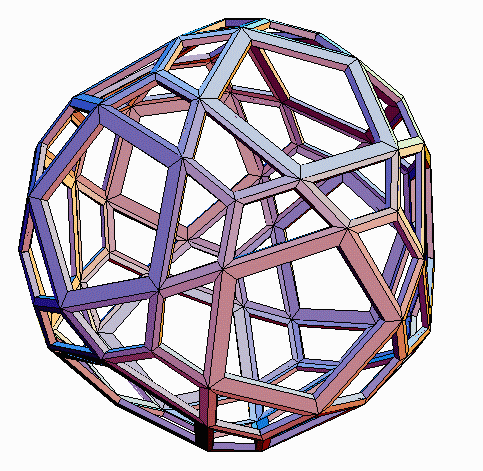
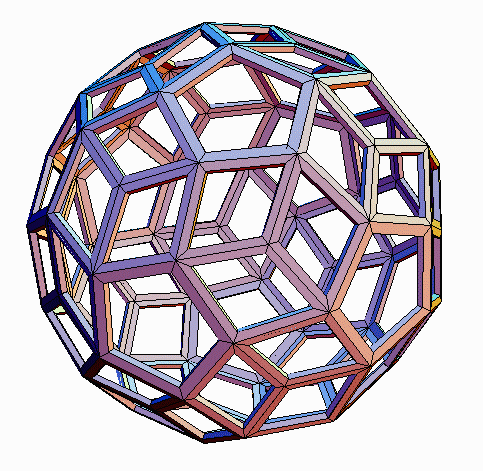
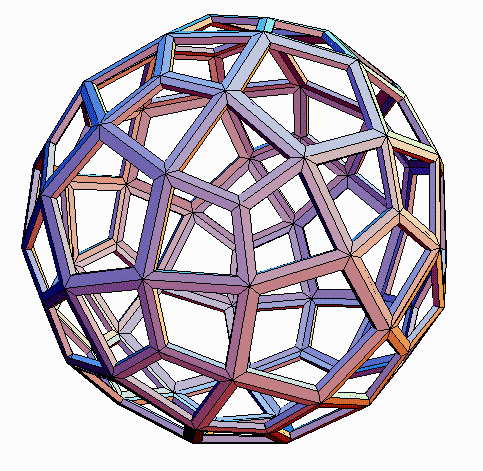
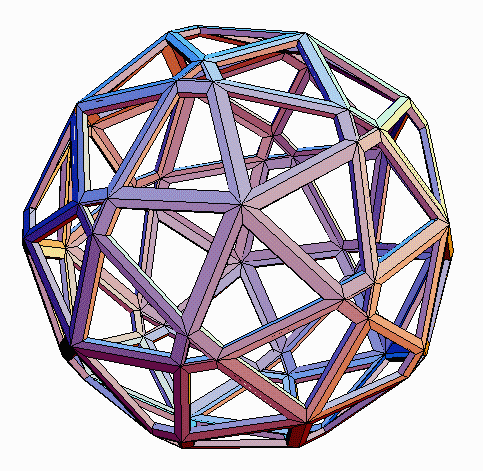
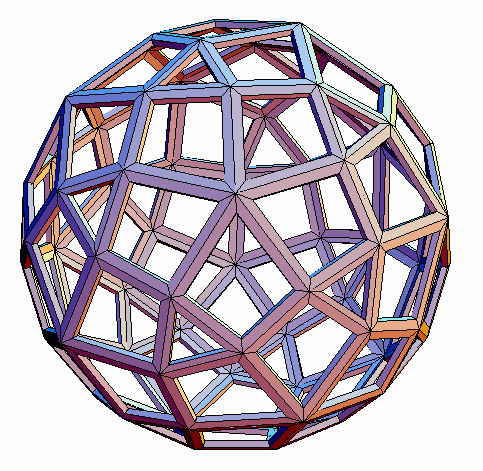
Starting from other polyhedra, the propellor operation gives other new
forms, each with a variety of geometric realizations. Figures 12-19 illustrate
the four remaining "propello-Platonics". The propello-cube (pC)
and propello-octahedron (pO) respectively have 30 faces (6 squares,
24 tetragons) and 32 faces (8 triangles, 24 tetragons). The propello-dodecahedron
(pD) and propello-icosahedron (pI) respectively have 72 faces
(12 pentagons, 60 tetragons) and 80 faces (20 triangles, 60 tetragons).
In all midscribed propello-Platonics, the tetragons are tri-equiangular
kites. In Figures 14-19, inscribed, circumscribed and midscribed versions
of the pD and pI are illustrated, showing the different shapes
of tetragons which can arise: tri-equilateral trapezoids, kites, and tri-equiangular
kites, respectively.
 |
 |
|
|
|
 |
|
|
 |
 |
|
|
|
 |
|
|
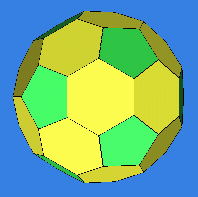
John Conway (personal communication) has devised a handy notation that is briefly sketched in this paragraph. The above propellor operation fits nicely into his framework. In Conway's notation, uppercase letters refer to standard polyhedra and lowercase letters refer to operators. Let T, C, O, D, and I stand for the tetrahedron, cube, octahedron, dodecahedron, and icosahedron, respectively. The operation d produces the dual, for example, dC=O is a statement that the dual of the cube is the octahedron. Letting X be a variable which ranges over polyhedra, ddX=X is a statement of the theorem that the dual operator is of order two. Another useful operator is the truncation operator t, for example, tI gives the truncated icosahedron (soccer ball shape) of Figure 20. Related to this is the "kis" operator, k, which is defined so kX is the polyhedron that results when a pyramid is erected over every face of X. Generally, kX=dtdX, for example, kC (what Conway calls the "kis-cube," usually called the "tetrakis cube") is the Catalan solid dual to the truncated octahedron. The "ambo" operation, a, is truncation to the edge midpoints, for example, aC is the cuboctahedron, and the "join" is defined by jX=daX. The "snub" operator, s, is what produces the snub cube, sC. It can be shown that aX=adX and sX=sdX. The "expand" operator, e, is "Mrs. Stott's expansion of faces" which separates faces and introduces rectangles for each edge, for example, eC is the rhombicuboctahedron. Conway has discovered the pretty fact that eX=aaX.
In this context, I use p to denote the propellor operation. One can show generally that p commutes with d and with a, i.e., pdX=dpX and paX=apX. From this it follows that pC and pO are mutually dual. Similarly, pI and pD are mutually dual.
 |
 |
 |
|
|
|
|
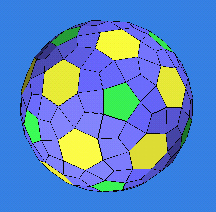
This notation succinctly describes complex combinations of operations. For example, Figures 20-22 show steps in the generation of the eptI ("expanded propello-truncated icosahedron"). Starting with the tI, its 32 faces are surrounded with tetragons to make the ptI. In this "propello-Archimedean," a propellor consists either of a pentagon and the five surrounding tetragons or a hexagon and the six surrounding tetragons. There are 32 propellors. Finally, expanding this ptI gives the eptI of Figure 22.
Intrigued by the power of Conway's notation, I have created generative
software that produces a polyhedron from its notation. On the web page
[10] one can simply type the expression "eptI" and the software generates
the object in Fig. 22 and displays it in the viewer's web browser. Similarly,
typing "edspT" causes the software to generate the "expanded-dual-snub-propello-tetrahedron"
shown in Fig. 23. Conway defines a "gyro" operator, g=ds,
so Fig 23 is also egpT.
 |
|
|
With the above background, the forms of a number of my sculptures can be concisely described and better understood. See [1] for additional photos and construction details.
The CD sculpture Rainbow Bits, Fig. 1, is based on the midscribed propello-icosahedron, pI, of Fig. 19. Carlo Sequin commissioned this piece for the Computer Science building at the University of California at Berkeley. This six-foot diameter sculpture hangs 20 feet up in an atrium of Soda Hall. I cut slits in the 642 CDROMs at my studio in New York and shipped them to California in a box smaller than a one foot cube. There, I assembled sub-units on the ground, raised them up in a lift, and assembled the sculpture in place, bonding them with a solvent cement. The CDs are supported by thin stainless steel wires that connect to fiberglass rods in a supporting structure above the sculpture. The support is suspended by chain that allows the sculpture to rotate freely with the air currents. Viewer-controllable light dimmers on flood lamps allow passers by to adjust the lighting for rainbows, shadows, or reflections, which all change as the sculpture spins.
A simpler, wooden sculpture based on the midscribed pI is shown
in Figure 2. It is constructed from 300 beveled pieces of quarter-inch
thick cherry, and is 16 inches in diameter. Appendix 2 gives a template
for constructing this form. The plaque (holly and cherry) and ornamentation
(brass wire) above the polyhedron copy the style of Leonardo da Vinci's
drawings of polyhedra in the manuscript for Luca Pacioli's 1509 book De
Divina Proportione.
 |
|
|
The wooden sculpture Roads Untaken, Figure 24, is based on the
eptI
of Fig 22. There are 902 pieces of wood assembled as a 17 inch diameter
mosaic over a fiberglass sphere. The woods are yellowheart, paela, and
padauk, and the "grout" is made from walnut sawdust. The natural colors
of these woods (yellow, orange, and dark red) were chosen to create visual
paths on the surface. Because of the color scheme, the eye can follow light
colored roads between hexagons or pentagons, and dark colored roads between
triangles. The dark colored roads happen to outline the edges of the uniform
compound of six pentagonal prisms, so there is no possible dark path between
most pairs of triangles.
|
|
|
|
Figure 25 shows a pair which I call Yin and Yang, constructed from walnut and linden (7 inch diameter). These are two mirror image forms of the propello-octahedron, pO, inscribed in a sphere. Because O=aT and p commutes with a, it happens that pO=paT=apT. So this form provides the simplest example of the theorem paX=apX. Each has color symmetry: exchanging light and dark leaves the form unchanged.
Finally, a pair of stereolithography orbs is shown in Figure 26. In
both of these three-inch balls, the eye naturally follows the winding pathways
of the edges. The first is a thin hollow form based on eesD, in
which each edge is thickened in proportion to its length, producing a lace-like
surface. The second is based on the egpT form of Fig. 23. Each edge
is cast to the center of the sphere and the bulk of the volume consists
of long pyramidal openings that almost meet at the center. The computer-controlled
rapid-prototyping process builds 0.01 inch thin layers based on data files
that I produced with special-purpose software. The stereolithography in
these realizations uses a starch-based process sealed with cyanoacrylic,
developed by Zcorp. I call the pair Gonads of the Rich and Famous.
  |
|
|
Conclusions
The propellor operation can be used to generate a wide range of novel, attractive polyhedra. The propello-Platonics, in particular, have many interesting properties, but the idea can be applied to any convex polyhedron. These new forms are the foundation for a number of sculptures by the author. For additional images of the artwork illustrated here, other geometric sculpture, and further construction details, see [1].
Appendix 1: Proofs of statements made above are sketched in this appendix. This may suffice for the proof-oriented reader to produce the necessary details. For background on polyhedral geometry, see [11].
(1) The midscribed pT is unique. A theorem by Schramm states that any simply connected polyhedron has a unique "canonical form" in which each edge is tangent to a unit sphere and the center of gravity of the points of tangency is the center of the sphere. See [5] for references to this literature.
(2) The inscribed and circumscribed pT are not unique. There is a two-parameter family of "tetartoids" of the form gT with the rotational symmetry of T. Within this lies a one-parameter family that satisfies an extra condition that two of its three orbits of vertices are equidistant from the center. These are inscribable after truncating four vertices. The construction from the regular dodecahedron gives a special point in this one-parameter family. Duality gives the family of circumscribed versions.
(3) pT is topologically self-dual. This is shown by drawing on its Schlegel diagram. Place a dot in the center of each face and connect adjacent dots. The resulting graph has four 3-way vertices and twelve 4-way vertices, and is topologically equivalent to the original.
(4) The circumscribed and inscribed versions of pT are geometrically dual (reciprocals in a sphere). The truncation process of Figure 7 is dual to the "kis" process of figure 9, and the two starting points are dual.
(5) The midscribed pT is geometrically self-dual. In a polyhedron midscribed to a sphere, the intersection of each face with the sphere is a circle inscribed in the face. The geometrical dual can be formed by constructing perpendicular lines tangent to the sphere at the points where the edges touch the sphere.
(6) Certain other propello-platonics may be derived by analogous methods. An inscribed pD with tri-equilateral trapezoids for its tetragons, Fig. 14, can be derived by truncating the 5-fold vertices of Catalan's pentagonal hexacontahedron. Dually, a circumscribed pI, Fig. 18, can be derived by elevating pyramids over the pentagons of the snub dodecahedron.
(7) The tetragons of the midscribed propello-Platonics are tri-equiangular kites. The faces of any midscribed polyhedron are circumscribed about circles. You can show face angles to be equal by showing the distances from the vertices to the tangent points are equal. The propellor operation and the normalization to midscribed form both preserve the rotational symmetry of the underlying Platonic solid. An axis of 2-fold symmetry intersects an edge of a midscribed propello-Platonic at its midpoint (by symmetry). That is where it is tangent to the sphere (otherwise, by symmetry, the edge would have two tangent points) hence two of the kite's angles are equal. The third follows from the regular polygons circumscribed about circles, therefore tangent at their edge midpoints.
(8) pdX=dpX and paX=apX. Draw a portion of generic polyhedral graph, carry out both operations, and see that the two results agree.
(9) If X has F faces, V vertices, and E edges, then pX has F+2E faces, V+2E edges, and 5E edges. This follows immediately from the construction; see, e.g., Fig. 4.
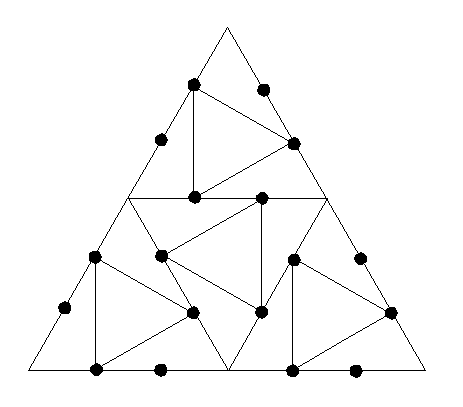
Appendix 2: The templates in Figure 27 are for the midscribed
propello-icosahedron in Leonardo's open-faced style. To make a paper model
of this form, make enlarged photocopies of these shapes onto card stock,
cut out 20 triangles and 60 tetragons, slice out the interior of each face
with an "exacto knife," and tape the pieces together following the pattern
shown in Fig. 2 or 19.
 |
|
|
References