George W. Hart

This is a large two-part sculpture I made at Middlesex
University in London in February, 2015. It is made of
laser-cut plywood joined by cable ties, part of a series of
designs I have been exploring using these materials.

Each of the two orbs is more or less an oblate spheroid, two
meters in diameter and one meter tall. They are mirror
images of each other, like a left-handed and a right-handed
glove.

Thank you to all the students and faculty in the School of Science and Technology who participated in this project, especially to Alison Megeney, who invited me and organized everything wonderfully and to Neil "Spike" Melton, who supervised the laser-cutting, sanding, installation, and other shop work.

If you are in New York, you can visit this reduced-scale prototype I made before flying out to England. This four-foot-diameter version is hanging in the artium of Packer Collegiate Institute in Brooklyn Heights. I built it with students in Brendan Kinnell's Art and Math class as a way of verifying the design and practicing the assembly process. Thank you to Brendan and the students for all your work in putting this together.


We assembled the orbs with the help of
many students and faculty. There are six shapes of
pieces that need to be connected with each other properly,
so it took lots of time and careful organization.
The initial step was to make three-part modules, which are
being assembled here to make the larger structure.

After several days of preparing the components, the assembly was spread over two days. We made one orb on each day. Here, the final modules being attached in the second orb on the second day.


When completed, we cut the tails off the cable ties and put the two orbs out on display. It takes most people some time to see that they are not identical, but are mirror images of each other.

Here is one orb, which we can arbitrarily call "right-handed". Observe the direction of the curves. (You can also observe how the mating edges of the parts were beveled, so they fit together precisely.)

The other orb, the "left-handed" one, has parts that curve the other direction. The exact same part shapes are used in each case, but they are flipped over and beveled on the opposite side for one orb.

Here's a rendering of the design looking down from the
top to show its five-fold axis of rotational
symmetry. The sculpture derives from an
underlying design that is spherical, and so looks
round like this from many directions, but I compressed
it by a factor of 1/2 along one axis to flatten
it. There are sixty identical components in the
underlying spherical form, but they are compressed
various amounts in various directions, depending on
how they are angled relative to the axis of
compression.
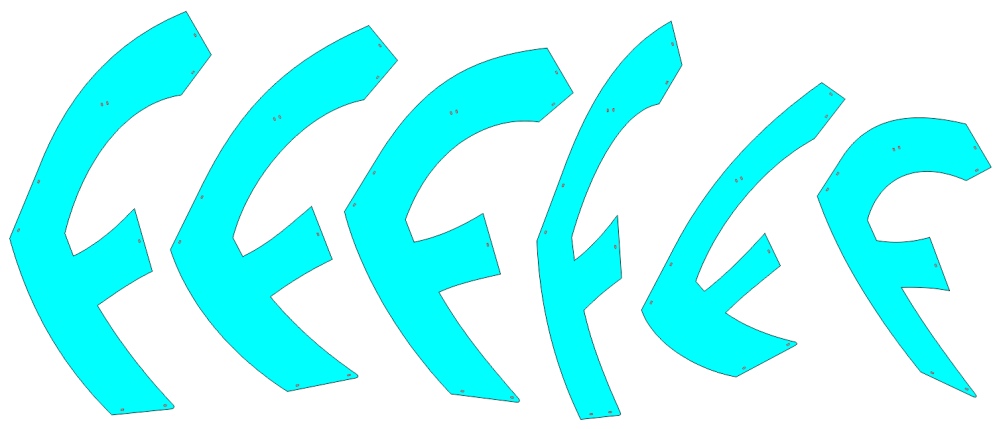
It turns out that there are six shapes of pieces after the compression, shown above. Ten of each are required for one orb. They are all "affine equivalent", which means they can be stretched in a linear way to become congruent to the others. There is also a complex combination of dihedral angles between the planes after compression, so it took a lot of care to bevel all the mating edges properly.

The sculpture is called Sword Dancing because the pieces are reminiscent of a kind of traditional ceremonial sword shown on the Middlesex University logo. Sword dancing is a fascinating activity in which performers make geometric structures from swords. If you are unfamiliar with sword dancing, see this video I made, which explains some of the underlying math. The sculpture was not designed with the University's logo's swords in mind; we realized the connection only after the sculpture was assembled.


After several days of preparing the components, the assembly was spread over two days. We made one orb on each day. Here, the final modules being attached in the second orb on the second day.

The assembly is an intricate group
puzzle that challenges everyone to intuit the
underlying structure of the form. For each
piece, there are two coplanar pieces in its plane and
three more pieces in a parallel opposite plane.
The parts are laser-cut from 6 mm thick plywood and
mitered to join very precisely. By looking
carefully, it is easy to distinguish between a part
that is positioned properly and one that is
incorrectly placed.

When completed, we cut the tails off the cable ties and put the two orbs out on display. It takes most people some time to see that they are not identical, but are mirror images of each other.

Here is one orb, which we can arbitrarily call "right-handed". Observe the direction of the curves. (You can also observe how the mating edges of the parts were beveled, so they fit together precisely.)

The other orb, the "left-handed" one, has parts that curve the other direction. The exact same part shapes are used in each case, but they are flipped over and beveled on the opposite side for one orb.

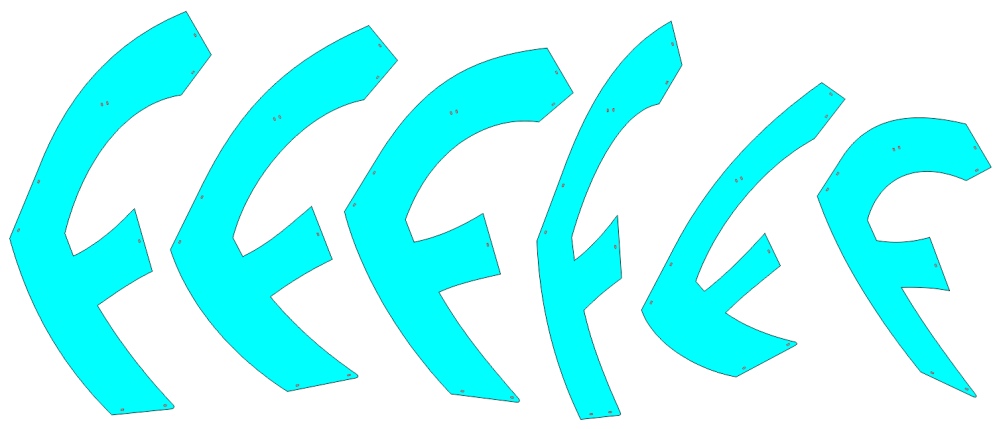
It turns out that there are six shapes of pieces after the compression, shown above. Ten of each are required for one orb. They are all "affine equivalent", which means they can be stretched in a linear way to become congruent to the others. There is also a complex combination of dihedral angles between the planes after compression, so it took a lot of care to bevel all the mating edges properly.

The sculpture is called Sword Dancing because the pieces are reminiscent of a kind of traditional ceremonial sword shown on the Middlesex University logo. Sword dancing is a fascinating activity in which performers make geometric structures from swords. If you are unfamiliar with sword dancing, see this video I made, which explains some of the underlying math. The sculpture was not designed with the University's logo's swords in mind; we realized the connection only after the sculpture was assembled.

If you are in
London, you can see Sword Dancing in the Hatchcroft
Building at Middlesex University.
For more about my laser-cut wood and cable-tie sculpture,
see this
paper from the Bridges 2015 conference.
There is a video about the design here.
Thank you to all the students and faculty in the School of Science and Technology who participated in this project, especially to Alison Megeney, who invited me and organized everything wonderfully and to Neil "Spike" Melton, who supervised the laser-cutting, sanding, installation, and other shop work.
If you are in New York, you can visit this reduced-scale prototype I made before flying out to England. This four-foot-diameter version is hanging in the artium of Packer Collegiate Institute in Brooklyn Heights. I built it with students in Brendan Kinnell's Art and Math class as a way of verifying the design and practicing the assembly process. Thank you to Brendan and the students for all your work in putting this together.
(Here's a math fact to think about:
Because it is 2/3 of the diameter of a full-scale orb, it is
less than 30% of the volume!)


For the 2016
Joint Math Meeting Art Exhibition in Seattle,
Washington, I made a smaller table-top version of the
design. It is dyed orange and is 18 inches in
diameter, standing 12 inches tall on its base. I can
proudly report that Sword Dancing won the prize
for best sculpture. You can get a better sense of
its structure in this video.