This is a webbified version of a paper in the Proceedings of

Art + Math = X International Conference in honor of Michele Emmer on his 60^th Birthday

June 2-5, 2005, University of Colorado at Boulder, pp. 88-92

Spaghetti Code: A Sculpture Barnraising

Computer Science Department

Stony Brook University

Stony Brook, NY, 11794, USA

Abstract

A two-meter diameter metal sculpture was assembled by a group of two hundred students, faculty, and staff at Stony Brook University on December 10, 2004. Its 180 laser-cut aluminum components were intricately woven through each other and locked together with 300 stainless steel pins. Although it may at first give the impression of a random spaghetti tangle, the form is highly structured mathematically. There are three shapes of parts (60 of each shape) and they are patterned with icosahedral symmetry (just the icosahedral rotations—not the reflections). The most surprising aspect of the design is that wherever two pieces join, they meet at a 90 degree angle. This allows the use of a very simple connector mechanism. After months of design and preparation, including the construction of a half-scale wooden version, less than two hours were required for the actual group assembly. It is now on permanent display suspended in the lobby of the Stony Brook Computer Science building.

1. Design

I construct geometric sculpture of various materials and like to engage groups of helpers in “sculpture barn raisings” [1-4]. Spaghetti Code, shown in Figure 1, is my latest example. The term Spaghetti Code is computer science jargon for a poorly organized program, but the sculpture is actually highly organized.

Figure 1: Spaghetti Code, aluminum, 2 meter diameter.

Spaghetti Code is constructed of 180 laser-cut, flat, aluminum parts. The form was carefully optimized over several months both for its aesthetics and to allow rapid, secure assembly. When designing sculpture to be constructed from rigid parts, the connections are a difficult issue that must be thought out carefully. My solution in this case was 300 simple mortise and tenon joints, locked with stainless steel cotter pins. A major difficulty with this approach is that, because of the nature of laser-cutting, both the mortise (a rectangular slot) and the hole in the tenon for the locking pin must be at 90 degrees to the material. Consequently, these joints require mating parts to lie in orthogonal planes. It would be easy to design a cube or rectangular box under this constraint, but I puzzled quite a while about how to make an intricate yet well-connected form with icosahedral symmetry using only 90-degree connections.

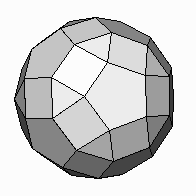
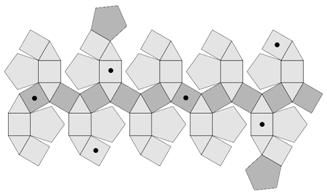
Figure 2: Rhombicosidodecahedron (RID) and its net.

To understand the many 90-degree angles in Spaghetti Code, it may help to begin with the rhomb-icosidodecahedron (RID) of Figure 2. This well-known Archimedean solid comprises 12 pentagons, 20 triangles, and 30 squares. It is not obvious that many pairs of faces lie in planes that intersect each other at 90 degrees. The unfolded net of the RID in Figure 2 illustrates this by shading two opposite pentagons, positioned as a North and South pole, and an “equator” of ten squares. The equatorial squares are halfway between the poles, so their planes lie at 90 degrees to the shaded pentagons’ planes. Because of the symmetry of this polyhedron, we could choose among six different pairs of pentagons to be the poles, each defining an equator of squares. This provides 120 pairs of orthogonal planes. There are also many 90-degree relationships between planes of two square faces. A careful study of the RID shows that the six squares marked with a dot in the net lie in the face planes of a cube, so provide twelve orthogonal pairs. There are five cubes among the 30 squares, providing in total 60 such pairs of orthogonal planes.

To take advantage of these 180 orthogonal plane pairs, the design of Spaghetti Code has 60 components in the twelve planes of the pentagons of one RID (five per pentagon) and has 120 components in the thirty planes of the squares of a larger concentric parallel RID (four per square). Selecting planes from two sizes of RIDs allows extra design freedom, yet scaling a set of planes radially inward or outward is only a translation so neither destroys the symmetry nor changes the 90-degree angle between planes. A total of 300 connections was achieved by having two pairs of parts join at some of the pairs of planes.

To develop the detailed form and arrange for the components to pass around others that lie in non-orthogonal planes, I used the software of [2]. This software allows the visualization and editing of symmetric sculpture, and outputs geometric description files in formats suitable for laser-cutting and solid freeform fabrication. The parts were fabricated at a commercial laser-cutting service bureau from 0.1-inch thick aluminum (6061-T6 alloy) and given a surface brushing on the outer side, which creates a gleaming visual effect. Preparation also included deburring the parts and drilling holes in five of them for suspending from chains. Before the assembly, I was able to promote the event with computer renderings such as Figure 3 and a small physical model. The solid freeform fabrication model, made of nylon by selective laser sintering, is shown in Figure 4.

Figure 3: Computer rendering.

Figure 4: Laser-sintered nylon model, 3 inches.

As a final preparation step, I laser-cut parts for a half-scale version in quarter-inch Baltic birch plywood. This allowed me to test the assembly sequence, confirm the five suspension points, and verify that I made no gross miscalculations, before committing to the expense of laser cutting the metal parts. Figure 5 shows the assembled wooden version. Its tenons are locked with 300 small wooden wedges.

Figure 5: Wood version, 1 meter diameter.

2. Barn Raising

The December 10, 2005 assembly event was attended by about 200 people—students, faculty, and staff at Stony Brook University. In the lobby of the Computer Science building where the sculpture now hangs, I asked groups of three students to work as teams as I gave directions. We first made triangular units in the air, seen in Figure 6. These units can be understood as cut out from the corners of a cube. After I checked that the parts were correctly arranged, they were locked together with stainless steel cotter pins. (A common error was making a mirror image of the desired configuration.) Then additional parts were added so the triangles were expanded first into six-piece units and then nine-piece units, e.g., Figure 7. Some tricky interweaving is required, but the shapes only fit snugly in one configuration. Again, after I checked for correctness, cotter pins locked the units. Twenty units are required for the complete sculpture.

Figure 6: Initial step of forming triangles.

Figure 7: Completed nine-part module.

The nine-piece units each have a 3-fold axis of symmetry and correspond in the overall structure to one triangle of an icosahedron. Using a temporary suspension point in easy reach near the ground, we started assembling the units together. Figure 8 shows a point where the top five modules are assembled to form a dome and the next layer is being added. Again, some intricate weaving is required to position the parts properly, but I was able to direct from the center of the structure while groups of students worked around me. Figure 9 shows the insertion of cotter pins and gives a view of the mortise and tenon joints.

Figure 8: Five modules form a dome.

Figure 9: Inserting cotter pins.

The adding and locking of modules continued until its icosahedral form was complete. Total assembly time was under two hours. We easily hauled its 80 pounds up to a hook that had previously been installed in the ceiling to hold it. Figure 10 shows the view looking up along a 5-fold axis from directly below.

Figure 10: Completed sculpture, viewed from directly below.

3. Conclusions

Spaghetti Code now hangs in the computer science building lobby at Stony Brook University, for all to enjoy. The feedback I received from participants confirms that everyone enjoyed being part of the sculpture barn raising. Often, I have seen people stop under it, point upwards, and tell their friends how they helped put it together. They feel an ownership in their sculpture. I had envisioned the sculpture as a fusion of high tech and baroque, both mathematical and organic. And I am very happy with both the sculptural result and the wonderful event at which it came into being.

References

[1] G. Hart, "The Millennium Bookball," Proceedings of Bridges 2000: Mathematical Connections in Art, Music and Science, Southwestern College, Winfield, Kansas, July 28-30, 2000, and in Visual Mathematics 2(3) 2000, and at http://www.georgehart.com

[2] G. Hart, "Sculpture from Symmetrically Arranged Planar Components", in Meeting Alhambra, (Proceedings of ISAMA-Bridges 2003, Granada, Spain), Javier Barrallo et al editors, Univ. of Granada, 2003, pp. 315-322.

[3] G. Hart, "A Reconstructible Geometric Sculpture", Proceedings of ISAMA CTI 2004, DePaul University, June 17-19, 2004, Stephen Luecking ed., pp. 141-143.

[4] G. Hart, "A Salamander Sculpture Barn Raising", Proceedings of Bridges 2004: Mathematical Connections in Art, Music, and Science, Southwestern College, Winfield, Kansas, July 2004, and in Visual Mathematics 7, no. 1, 2005.

Acknowledgements: Thank you Arie Kaufmann for finding funds to cover the materials. Thank you Jim Quinn for making the SFF model of Figure 4. Thank you Erik and Martin Demaine for letting me use a laser-cutter at MIT to make the parts for Figure 5. And thank you especially to everyone who participated in the assembly!

More images are available online here.