Canonical Polyhedra
 An
interesting theorem states that there exists a "canonical form" of any
given convex polyhedron. This canonical form is a possibly distorted version
of the given polyhedron in which the vertices are positioned in space to
satisfy the following properties:
An
interesting theorem states that there exists a "canonical form" of any
given convex polyhedron. This canonical form is a possibly distorted version
of the given polyhedron in which the vertices are positioned in space to
satisfy the following properties:
- all the edges are tangent to the unit sphere,
- the origin is the center of gravity of the points at which the edges touch the sphere,
- the faces are flat (i.e. the vertices of each face lie in some plane), but are not necessarily regular.
The familiar symmetric polyhedra, e.g., Platonic, semi-regular, or Archimedan duals, already satisfy the three properties above, and so are already in their canonical form. But an arbitrary "random" polyhedron needs to be adjusted to get into this form. One application of this is that given a new irregular-looking polyhedron, one can find its canonical form and look at it to see if it is the same as a previously familiar canonical form.
To appreciate what this is all about, we can look at some examples of a not too regular polyhedron and its canonical form. The Johnson solids are good polyhedra to start with. The following examples show an original version and its canonical form. Be sure to notice that if the original has any planes or axes of symmetry, then the canonical form preserves those symmetries.
- elongated pentagonal gyrobirotunda (J43), canonical form
- metabidiminished icosahedron (J62), canonical form
- biaugmented truncated cube (J67), canonical form
- snub disphenoid (J84), canonical form
- disphenocingulum (J90), canonical form
- bilunabirotunda (J91), canonical form
 For
some additional examples:
For
some additional examples:
- start with this random seven-zone zonohedron (as seen on the zonohedron page) to get this canonical form (shown at the top of this page). Observe that the result has central symmetry just as the original zonohedron does.
- start with a tetrahedrally stellated icosahedron to get this canonical form with chiral tetrahedral symmetry, i.e., no planes of symmetry. It is particularly interesting because it is self-dual. Here is it compounded with its dual, as illustrated at right. You can also get here starting from the tetrahedrally truncated dodecahedron. (More about these polyhedra.)
- check out this 22-sided polyhedron which I cooked up to see something else with tetrahedral symmetry, but chiral. It began as a truncated octahedron with four hexagons trisected.
-
start with a cube from which one corner has been maximally truncated, to
get this heptahedron in canonical
form. The 4-sided faces are like half a cube and the 3-sided faces
are like half an octahedron, so its dual is the same polyhedron, but "turned
over." When we combine
it with its dual, the result contains two half-cubes and two half-octahedra,
like yet unlike the compound
of a cube and octahedron.
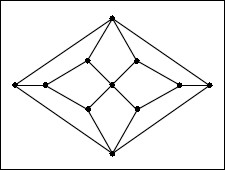
- start with the net shown here (Figure 1.5A of Coxeter's Regular Polytopes, p.8), to get this nice enneahedron. It is interesting because it is the simplest polyhedron for which there is no Hamiltonian cycle (a round trip via edges which visits each vertex exactly once). What is more interesting is that from the net it is not at all apparent that the solid has 3-fold symmetry, but the canonical form brings it out immediately. (I was surprised !) I believe it is also the simplest polyhedron with an odd number of faces that each have the same number of edges.
- next, here is a canonical form of a "heptagonal hermaphrodite." It is composed of half a prism and half a dipyramid. The result is self-dual, so it makes a nice compound with itself.
- and finally, here is the canonical form of a "heptagonal antihermaphrodite." It is composed of half an antiprism and half a trapezohedron. The result is again self-dual, so it also makes a nice compound with itself.
My canonicalizing algorithm inputs a polyhedron (or "3-connected" planar graph) and computes its canonical form numerically. I used it to produce the canonical forms above (and many others, for testing purposes.) The algorithm inputs a polyhedron (or maps a graph around the unit sphere to create a set of vertices and edges) and then iteratively modifies it to improve its conformance with the three conditions at the top of this page. After a couple of hundred iterations it typically finds that the conditions are satisfied within a very small tolerance, and stops. Three simple operations are all that is needed; they correspond to the three conditions:
- For each edge, the closest point to the origin is determined, call it x. If x lies at unit distance from the origin, the first condition is satisfied for that edge. If not, a small fraction of x is added to the two vertices which define the edge, (in proportion to the sign and amount of the error) so that at the next iteration the edge will be closer to tangency with the unit circle.
- The center of gravity of all the points x is determined. If it is zero, the second condition is satisfied. If not, it is subtracted from all the vertices.
- For each face, if the vertices lie in a plane in space, the third condition is satisfied. If not, a plane which approximates it is computed. (Rather than a least-squares fit, a quick method is used: the average of the cross products of the face angles defines a normal direction and the centroid of the face's vertices defines a distance from the origin.) Each vertex of the face is then projected on to the plane.
Mathematica code is available in the article Hart [1997] listed in the references.