Known
to the ancient Greeks, there are only five
solids which can be constructed by choosing a regular convex
polygon and having the same number of them meet at each corner:
- The cube has three squares at each corner;
- the tetrahedron has three equilateral triangles at each corner;
- the dodecahedron has three regular pentagons at each corner.
- With four equilateral triangles, you get the octahedron, and
- with five equilateral triangles, the icosahedron.
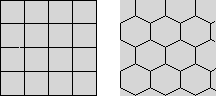No
other possibilities form a closed convex solid. For example, four squares
or three hexagons at each corner would result in a flat surface, like floor
tiles.
It is convenient to identify the platonic solids with the notation {p, q} where p is the number of sides in each face and q is the number faces that meet at each vertex. Thus, the cube is {4, 3} because it consists of squares meeting three to a vertex.
Exercise: Give the {p, q} notation for all five Platonic solids.
Answer: Always do these exercises yourself before looking at my answer.
Observe that if {p, q} is a possible solid, then so is {q, p}.
In nature, the cube, tetrahedron, and octahedron appear in crystals. The dodecahedron and icosahedron appear in certain viruses and radiolaria. Note that names such as dodecahedron are ambiguous; sometimes the regular dodecahedron is meant and sometimes the word refers to any of the many polyhedra with twelve sides.
Exercise: Get to know these polyhedra and the relationships between them by counting the number of faces, edges, and vertices found in each of these five models. Make a table with the fifteen answers and notice that only six different numbers appear in the fifteen slots.
Answer: Fill in this table before looking at my answer: