Truncated Hexa-Octahedron Zome Model	Truncated Hexa-Octahedron (from reference cited below)

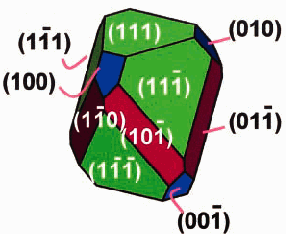
In an inspiring piece of geometric detective work, a polyhedral shape has led scientists to conclude that life existed on Mars.  An article by NASA astrobiologist Kathie L. Thomas-Keprta and nine coauthors, titled "Truncated hexa-octahedral magnetite crystals in ALH84001: Presumptive biosignatures," appeared in the Proceedings of the National Academy of Science, Vol. 98, Issue 5, 2164-2169, February 27, 2001.  The image at right above and two similar images below come from their paper.

These scientists have studied a meteorite which originated on Mars 4.5 billion years ago and fell to Earth in Antarctica.  The meteorite contains microscopic crystals of magnetite of a distinctive form.  They report that this crystal shape is not formed by any known inorganic process.  This shape of magnetite crystal is only found on Earth when formed inside certain bacteria that use it internally as part of their mechanism for aligning with magnetic fields.  These bacteria evolved to produce this form because it is very efficient for this purpose.  They conclude that the most likely explanation for its appearance in a Martian meteorite is that these crystals were formed inside bacteria living on Mars which also evolved to produce this form.

The telltale shape is called the truncated hexa-octahedron.  Before making a Zome model of it, first make and understand a plain hexa-octahedron.  This hexa-octahedron has the form of a regular octahedron which is expanded in the direction of one of its 3-fold axes, producing six new parallelogram faces.  (As such, it falls in the class of polyhedra which I call zonish polyhedra---the parallelograms form a zone which separates the two halves of the octahedron.)
 

Four faces of a regular octahedron	Hexa-octahedron

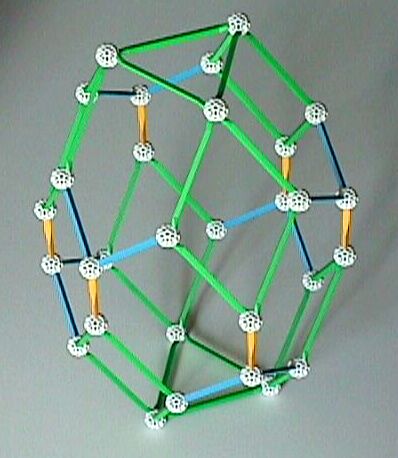
1. Hexa-octahedron. Make a regular g1 octahedron, rest it on a face, and notice the zig-zag hexagon which divides it into two groups of four faces.  Remove the three edges of the top triangle, leaving just the bottom four triangles and their zig-zag rim as shown above at left.  Insert a y2 vertically into each of the six Zomeballs.  Six balls at the top of these six yellows provide the vertices for the second octahedron half. (The two halves could be separated an arbitrary distance while remaining parallel.)  The result is called a hexa-octahedron because there are six faces of one type (green and yellow parallelograms) and eight faces of another type (equilateral triangles).

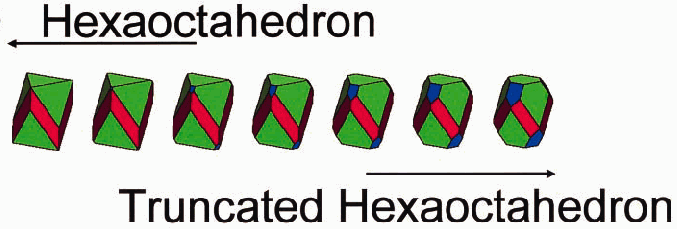
2. Truncated hexa-octahedron.  Illustrated at the top of this page, this derives from the hexa-octahedron by cutting off the three top corners and three bottom corners.  This truncation can be done so the six new faces lie in the planes of a cube.  (They are blue in these images from the paper. Two opposite blue planes are parallel; any other two blue planes are perpendicular, exactly as in a truncated octahedron.)  It should be straightforward to construct a Zome model from the figure at the top left of this page, knowing the following: The top and bottom faces are irregular hexagons with six equal angles, constructed as g1-g2-g1-g2-g1-g2.  The six truncation faces (in the planes of a cube) are constructed as g1-g1-g1-b1-b1 (adjoin a g1 square and half a b1 square).  The six  remaining pentagons are g3-g3-g1-g2-g1 (where g3=g1+g2, of course).  And finally, the six yellows struts that connect the two halves of this structure could be of any length; here they are y1.
 

Variant with deeper truncation

3. Deeper truncation.  Above is a third variant, in which the truncations are so deep as to meet, making the top and bottom faces triangles, rather than hexagons.  This may be too deep to be physically appropriate, but it is good to understand this limiting case.  The figure below illustrates a form which comes very close to this.

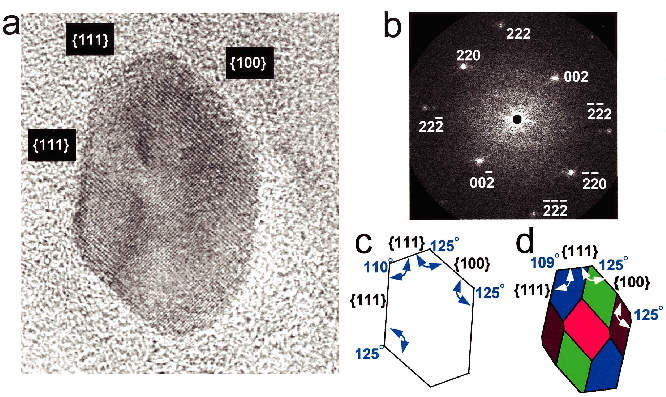
McKay et al. [(1996) Science 273, 924-930] suggested that carbonate globules in the meteorite ALH84001 contained the fossil remains of Martian microbes. We have characterized a subpopulation of magnetite (Fe3O4) crystals present in abundance within the Fe-rich rims of these carbonate globules. We find these Martian magnetites to be both chemically and physically identical to terrestrial, biogenically precipitated, intracellular magnetites produced by magnetotactic bacteria strain MV-1. Specifically, both magnetite populations are single-domain and chemically pure, and exhibit a unique crystal habit we describe as truncated hexa-octahedral. There are no known reports of inorganic processes to explain the observation of truncated hexa-octahedral magnetites in a terrestrial sample. In bacteria strain MV-1 their presence is therefore likely a product of Natural Selection. Unless there is an unknown and unexplained inorganic process on Mars that is conspicuously absent on the Earth and forms truncated hexa-octahedral magnetites, we suggest that these magnetite crystals in the Martian meteorite ALH84001 were likely produced by a biogenic process. As such, these crystals are interpreted as Martian magnetofossils and constitute evidence of the oldest life yet found.

The complete paper and other related astrobiology reports about this meteorite can be found on NASA's web site.