
Each year I visit Mathcamp for a week to lead some fun hands-on activities.
Here's the complete graph on eleven vertices, one of two ribbon constructions we made.

We also made a lovely expanded 120-cell model from Zometool.

And we had a bagel-cutting workshop to make linked bagel halves and trefoil knots.

And here is a very tricky geometric construction from twenty identical pieces of paper.
The four activities shown above are detailed in the four sections below.
1. Paper Construction

This is a paper model of a sculpture I call Snarl.

I brought the cut paper parts, so the Mathcampers had "only" to assemble and tape them.

It is really hard, trust me! Getting the first cycle of five is the key step. Then add parts one at a time.

I made the paper model to help make the structure clear, but the "overs and unders" are subtle.

It is easier to do if one has an appropriate thinking cap.

I don't recommend this technique of trying to add the last five parts as a single module.

It is quite an accomplishment when done! Only a dozen or so people
in the history of the universe have ever succeeded in building this.

If you want to try assembling your own copy, this 3-fold axis view may be helpful.
But I warn you, it is hard. The template for the parts is here.
2. Bagel Cutting

In this workshop, I showed how to cut a bagel into two congruent linked halves.

Anyone can do it in ten seconds once they learn the steps.

An optional extra activity is to do the integral that gives the surface area of the twisted cut.
Here, the bagel itself was a convenient manifold for writing on, to work it out.

Despite having only tough non-New-York bagels, these came out quite well.
I have the instructions for cutting bagels into two linked halves online here.
And the instructions for cutting a trefoil knot bagel are online here.
3. Zometool Workshops

I always do an assortment of 3D and 4D construction workshops at Mathcamp.

These are dodecahedral modules for making the expanded 120-cell, an attractive 4D polytope.

With a lot of teamwork, the modules gradually come together over about four hours.

And here is the finished polytope, with me looking through it.
You can read about the fifteen Zome-constructable H4 polytopes here.
4a. Math Mob Complete Graph

The idea of a math mob is to propose a concept for a mathematical event
that is scalable so many people can come together and do something cool.
Here we will make K11 from pink "marking ribbon" used by surveyors.

After spacing ourselves into a circle, one person ties the end of the ribbon to his left wrist.

The ribbon is passed around and around. Initially it is tied to every person's left wrist.
On the second and third cycle, it is tied to every second person's left wrist. And so on.

Since eleven is prime, the algorithm is particularly simple in this case.

The chords get closer and closer to the center as the number of skips grows larger.

When complete, every person is connected to each of the other people in a large piece of "string art".

The view looking up from underneath is quite cool.

Anyone walking by is drawn in with an irresistible urge to stand in the center.

We walked inside while still wearing it. It pops nicely back into shape after going through doorways.
4b. Math Mob Parabola

As a second math-mob ribbon construction, we made a giant parabola.

The participants line up in two rays making 90 degrees, with the vertex at the top.
Passing the ribbon along the line, wrapping around the wrists, we construct a series of lines.

The amphitheater steps are helpful for equal spacing. The envelope of the lines is a parabola.
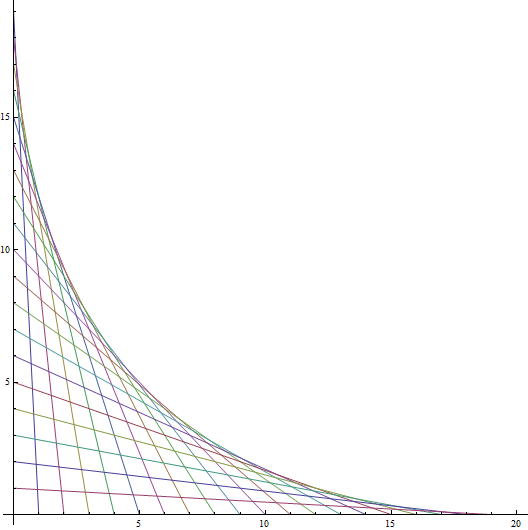
Above is the standard axes orientation. Can you prove these lines are tangent to a parabola?

Here is the final parabola.
(More math mob ideas are sketched here, which I may try somewhere on a future occasion.)