Pop Quiz Answer

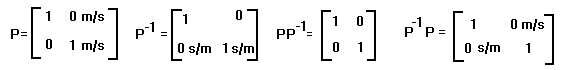
Two theorems relevent to the problems:

1. A square matrix has a determinant iff there is at least one matrix-matrix product in which it can take part. (But it might not be able to take part in a product with itself.)
2. It is usually the case that the product of a nonsingular matrix and its inverse in the two possible orders gives two different results. (As is familiarly the case with two matrices in which both orders of multiplication are defined.)

These are but two of many interesting properties which are obscured when one simply ignores the dimensional structure of vectors and matrices and works with numbers alone. A simple example solving both pop-quiz problems is

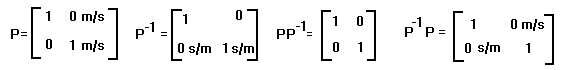
For proofs of the two theorems above, and a full discussion of the differences between traditional linear algebra and the algebra which scientists and engineers really use, see my book:

George W. Hart, Multidimensional Analysis: Algebras and Systems for Science and Engineering, Springer Verlag, 1995.

Back to the Multidimensional Analysis page.