Pentagrams
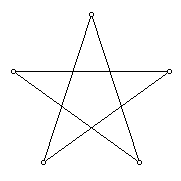 Pentagrams
are "five-pointed stars." They are regular polygons
with five vertices and five edges; that's all.
The sides just happen to cross each other at five points of intersection
which outline the small interior pentagon, but those are not vertices and
the smaller segments are not complete sides. Mathematically, the pentagram
is special for being the simplest nonconvex regular polygon.
Pentagrams
are "five-pointed stars." They are regular polygons
with five vertices and five edges; that's all.
The sides just happen to cross each other at five points of intersection
which outline the small interior pentagon, but those are not vertices and
the smaller segments are not complete sides. Mathematically, the pentagram
is special for being the simplest nonconvex regular polygon.
Technical note: Historically, the pentagram has been interpreted as having mystical power at least since Pythagorean times. In our time, the shape seems to hex many VRML browsers, which assume that all polygons are nonintersecting. You can see the occult effects in the solid with pentagrams below.
 Mathematically,
we want do describe pentagrams with only five vertices and five edges in
these VRML files. This would allow the file to be used as input to
various operations on polyhedra (such as truncation). However, most
VRML browsers have a problem with this, and we need to create a more complex
description of out pentagrams in order for them to display properly. To
see how your browser behaves, compare these three different versions of
the small triambic icosidodecahedron, which contains twelve pentagrams
and twenty triangles. (If you count sixty triangles rather then twenty,
then read this, but that is a different
issue.)
Mathematically,
we want do describe pentagrams with only five vertices and five edges in
these VRML files. This would allow the file to be used as input to
various operations on polyhedra (such as truncation). However, most
VRML browsers have a problem with this, and we need to create a more complex
description of out pentagrams in order for them to display properly. To
see how your browser behaves, compare these three different versions of
the small triambic icosidodecahedron, which contains twelve pentagrams
and twenty triangles. (If you count sixty triangles rather then twenty,
then read this, but that is a different
issue.)
- small triambic icosidodecahedron (with pentagrams) This file defines the pentagrams in the mathematically correct manner, as having five vertices and five edges. You will probably observe that two of the five concavities of each pentagram appear covered over. The problem is that most VRML browsers break the pentagram up into three triangles, two of which extend beyond the pentagram proper. Some VRML viewers produce an interesting change in the triangulation when one moves in close enough for the self-intersecting face to intersect the edge of the viewing window.
- small triambic icosidodecahedron (with concave decagons) This file attempts to correct the above problem by replacing the five-sided pentagram definitions with ten-sided non-convex polygons. (Switch to "wireframe view" if your browser has that option to see that the pentagrams are drawn with ten sides rather than five.) It appears that many (but not all) VRML browsers can handle concave pentagons as long as no two edges cross.
- small triambic icosidodecahedron (with triangulated pentagrams) What I have done here is replace each pentagram with five triangles, by adding a new vertex at the centroid of each pentagram. The triangles overlap in the center region, but that is not a problem. Again, you can see it clearly in wireframe mode.
As the first approach seems always to give problems, and the second
does in some browsers, I have used the third approach on all nonconvex
polygons here. I believe this is guaranteed to display correctly in all
viewers, but the cost is that all the files are somewhat larger, and are
more difficult to use for other mathematical applications. A program which
inputs one of these files to process it in some other way than just viewing
(e.g., to calculate its dual or a stellation, etc.) must do an extra step
to reassemble the five sub-faces into one non-convex face.