Glossary
This
page pertains to the parts and properties of polyhedra. Most of the entries
have links to more detailed discussions.
The naming of individual polyhedra is discussed
on its own separate page.
antiprism - A semi-regular polyhedron constructed from two n-sided polygons and 2n triangles. See the prisms and antiprisms entry.
Archimedean - The 13 Archimedean solids are convex semi-regular polyhedra.
canonical form - A form of any given polyhedron distorted so every edge is tangent to the unit sphere and the center of gravity of the tangent points is the origin. See the canonical form page.
chiral - Having different left-handed and right-handed forms; not mirror symmetric; opposite of reflexible. The cube is not chiral; the snub cube is chiral as these two versions of the snub cube illustrate.
compound - An assemblage of two or more polyhedra, usually interpenetrating and having a common center.
convex - A convex polygon or polyhedron contains no holes or indentions. If one constructs a line segment between any two points of a convex object, then every point on the line segment is part of the object. The pentagram is a non-convex polygon; the Kepler-Poinsot solids are non-convex polyhedra.
dihedral angle - The angle defined by two given faces meeting at an edge, e.g., all the dihedral angles of a cube are 90 degrees. Usually it is measured as the interior angle at the edge, so an almost-spherical polyhedron (with many faces) has a dihedral angles just under 180 degrees. But it can also be measured as the angle between lines perpendicular to the faces (i.e., the face normals), in which case a many-faced almost spherical polyhedron has dihedral angles close to zero.
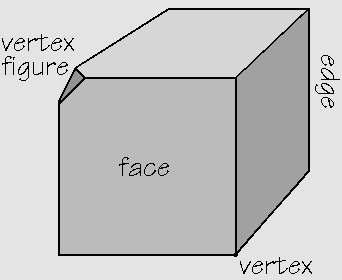
edge - A line segment where two faces meet. A cube has 12 edges.
enantiomorph - the mirror image of a given chiral polyhedron.
face - A polygon bounding a polyhedron. A cube has six square faces.
golden ratio - (1+sqrt(5))/2, approximately 1.61803, which happens to be the ratio of a diagonal of a pentagon to its side. This constant shows up in many metrical properties of the dodecahedron and icosahedron just as the square root of 2 shows up in the metrical properties of the cube. A golden rectangle has sides in this ratio. A golden rhombus has diagonals in this ratio.
net - a drawing of a polyhedron unfolded along its edges, to lay flat in a plane. The earliest known examples of nets to represent polyhedra are by Albrecht Durer.
pentagram - five-pointed star.
Platonic - Five fundamental convex polyhedra. They have regular faces and identical vertices.
polygon - A connected two-dimensional figure bounded by line segments, called sides, with exactly two sides meeting at each vertex.
polyhedron (plural: polyhedra) - A three dimensional object bounded by polygons, with each edge shared by exactly two polygons. Various authors differ on the fine points of the definition, e.g., whether it is a solid or just the surface, whether it can be infinite, and whether it can have two different vertices that happen to be at the same location.
prism - A semi-regular polyhedron constructed from two n-sided polygons and n squares. See the prisms and antiprisms entry.
quasi-regular - The edge-regular polyhedra within the uniform solids having special properties.
reflexible - Having a plane of mirror symmetry; opposite of chiral.
regular - A polygon is regular if its sides are equal and its angles are equal. A polyhedron is regular if every face is regular and if every vertex figure is regular. Standardly, there are nine regular polyhedra: the five Platonic solids and the four Kepler-Poinsot solids, but others might be allowed, depending on the definition of polyhedron.
rhombus (plural: rhombi ) - A polygon consisting of four equal sides, e.g., in zonohedra.
self-intersecting - A polygon with edges which cross other edges; a polyhedron with faces which cross other faces.
semi-regular - Consisting of two or more types of regular polygons, with all vertices identical. This includes the Archimedean solids, the prisms and antiprisms, and the nonconvex uniform solids.
stellation - The process of constructing a new polyhedron by extending the face planes of a given polyhedron past their edges. See, e.g., the 59 stellations of the icosahedron.
truncate - To slice off a corner of a polyhedron around a vertex. The figure at the top of this page shows a cube with one vertex truncated.
uniform - A uniform polyhedron has regular faces, with each vertex equivalently arranged. This includes the Platonic solids, the Archimedean solids, the prisms and antiprisms, and the nonconvex uniform solids.
vertex (plural: vertices) - A point at which edges meet. A cube has 8 vertices.
vertex figure - The polygon which appears if one truncates a polyhedron at a vertex. The figure at the top of this page shows that the vertex figure of the cube is the equilateral triangle. To be sure to be consistent, one can truncate at the midpoints of the edges.
zonohedron (plural: zonohedra) - A polyhedron in which the faces are all parallelograms or parallel-sided.