Additions to

Zome Geometry

George W. Hart and Henri Picciotto

A Couple of Confusing Compounds

If you like tricky puzzles, here are two that are a bit tougher than what is in the book. Each is an assembly of separate but identical components, which only stay in relative position because the struts touch each other. In both cases, the overall symmetry is chiral icosahedral.

1. Five Truncated Tetrahedra

If you enjoyed making the compound of five tetrahrdra (Unit 11.3) and the truncated tetrahdron (Unit 12.3) then you can imagine truncating the five tetrahedra to make the compound of five truncated tetrahedra. It is quite a challenge to weave the struts through each other properly. Use g2 struts. The five truncated tetrahedra, although not connected to each other via Zome balls, lock each other in place.


Image of compound of five truncated tetrahedra, showing how the faces intersect. (The yellow faces are hexagons; the red faces are triangles.)	Zome model of compound of five truncated tetrahedra, requires 90 g2 struts.

2. Six Pentagonal Prisms

Even trickier, here there are six pentagonal prisms, each with b3 pentagons for bases and r3 struts for the "vertical" edges. The 5-fold axis of each prism points in one of the directions of the six 5-fold axes of the whole compound. When properly constructed, it is very amazing how no two blue struts quite touch. The only contact between different prisms is where a blue strut touches a red strut near its center.


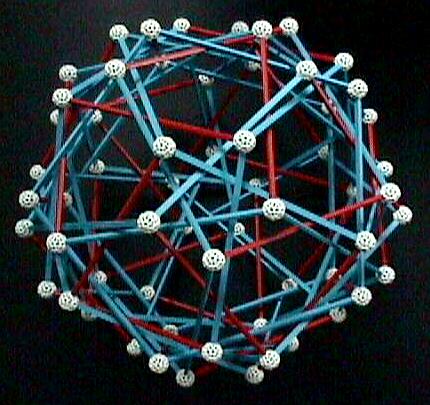
Image of compound of six pentagonal prisms, showing how the faces intersect. (The green faces are pentagons; the blue faces are squares.)	Zome model of compound of six pentagonal prisms, requires 60 b3 struts and 30 r3 struts. (The prisms' sides are rectangles, not quite squares.)

If you like these, I added two more tricky compounds here.